4. Inverseur de sources automatique
Un inverseur de source automatique (ATS: Automatic Transfer Switch en anglais) est un dispositif qui permet de commuter automatiquement et très rapidement (50 à 200 ms) une installation électrique depuis une alimentation principale (le réseau électrique) vers une alimentation secourue (groupe électrogène ou réseau de secours). Au coeur du dispositif se trouve typiquement un ou deux électroaimants “à noyaux plongeurs” pour opérer la bascule de l’inverseur.

Fig. 4.3 Un inverseur de source automatique. (cf. Commutateurs et inverseurs de sources Socomec)
4.1. Ressources sur les Inverseurs de sources
Aperçu du principe de fonctionnement en 4’
4.1.1. Socomec
https://www.socomec.fr/inverseurs-sources-automatiques_fr.html
Documents commerciaux du constructeur Socomec:
Diapos de présentation commerciale
"Commutateurs de sources"Extrait catalogue
"Solutions de commutation", avec en particulier :p 12-13 : aperçu des solution et définition des termes (MTSE, RTSE, ATSE)
p 47 : caractéristiques techniques de la gamme ATyS M (e.g. durées de commutation)
p 115-133 : Cahier Technique sur les inverseurs de sources (TSE)
4.1.2. ASCO Power Technologies
Le constructeur ASCO Power Technologies, racheté par Schneider électrique en 2017, a publié une série de livres blancs sur les ATS dont en particulier :
Transfer Mechanism Basics: transfer-mechanism-basics.pdf
Summmary: “Key components of transfer switch mechanisms include a solenoid that powers the operator mechanism(s) and its connected rotating shafts and weights. They also include the main and arcing electrical contacts and arc chutes. Open transition switches typically use a single operator and solenoid. Delayed Transition and Closed Transition switches use two-solenoid two-operator mechanisms. A complete transfer switching cycle provides two opportunities for arcing to occur across contacts. This first occurs when contacts approach closure. The second occurs as contacts open. These arcs can pit contact surfaces, which increases resistance and produces heat.”
(voir en particulier la figure 4 qui montre comment l’électroaimant en translation génère une rotation)
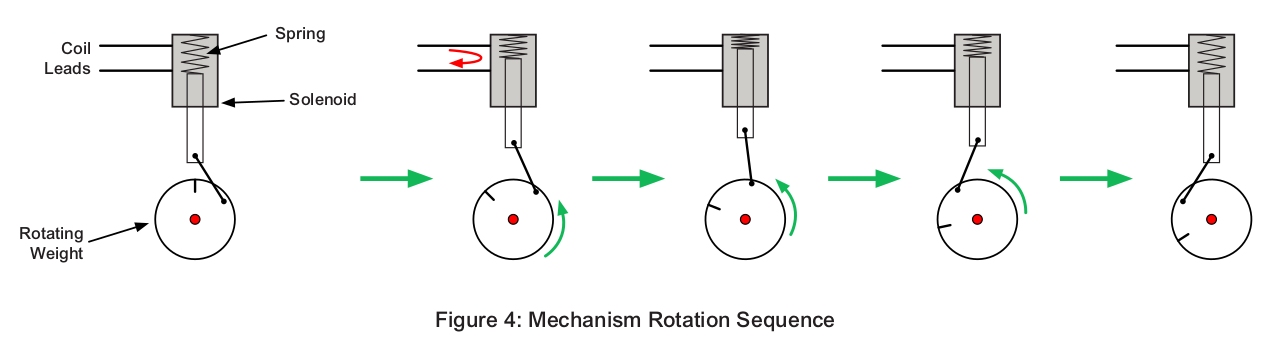
Fig. 4.4 ATS Mechanism Rotation Sequence (ASCO whitepaper)
Basic Control of Automatic Transfer Switches: basic-control-of-ATS.pdf
Summmary: “An automatic transfer switch (ATS) consists of two primary components, an electrically operated double-throw switch and a controller. Key controller functions include voltage monitoring, control signaling, timing delays, and switch mechanism operation. This paper describes how controllers monitor voltage, frequency, and phase angle differences between Normal and Emergency power sources, and explains how timing delays are applied to ensure the availability of reliable power.”
4.2. Objectifs de modélisation
La modélisation de l’électroaimant fera apparaître un aspect électrique, magnétique (réluctances) et mécanique en translation. Un mécanisme du type pignon-crémaillère ou bielle-manivelle transforme cette translation en rotation.
L’inverseur lui-même est un ensemble d’interrupteurs rotatifs (source 1 : -60°, source 2 : +60°). Un ressort permet de maintenir l’inverseur dans l’une ou l’autre des positions (TODO : schéma à faire) La commutation électrique sera modéliser au plus simple (sans effet d’arc électrique).
4.3. Description technique de l’ATS
4.3.1. Électroaimant à noyau plongeur
Pour réaliser un actionneur électriques linéaire pour des petits déplacements, on peut utiliser un électroaimant à noyau plongeur. Un tel aimant est schématisé Fig. 4.5. Il se compose de:
une partie mobile en translation, le noyau plongeur qui est un cylindre en matériau ferromagnétique. On note \(x\) sa position.
une partie fixe avec:
un enroulement qui entoure le noyau qui va générer un flux magnétique lorsqu’il est alimenté. On note \(n\) le nombre de spires et \(i\) le courant qui le parcourt.
une culasse ferromagnétique qui aide à canaliser l’induction magnétique. La culasse fait aussi butée pour le noyau en \(x=0\).
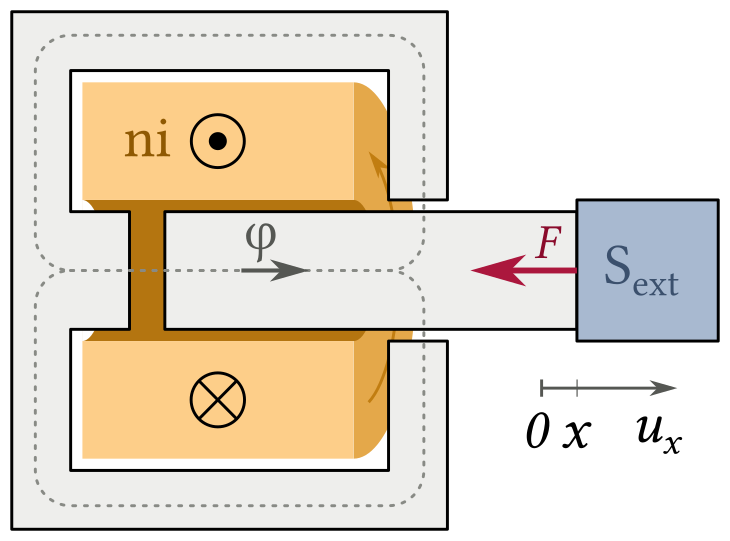
Fig. 4.5 Schéma de l’électroaimant à noyau plongeur. Le système est axisymétrique (invariant par rotation autour de l’axe central de déplacement du noyau)
Calcul de la force exercée par le noyau de l’électroaimant sur un object extérieur qui lui est attaché:
où \(W'\) est la coénergie du système et \(L(x)\) l’inductance propre de l’enroulement, qui dépend de la position du noyau. Remarque : l’expression fonction de l’inductance n’est vraie que si on néglige la saturation.
L’inductance est une fonction décroissante de la position du noyau, donc la force \(F\) est négative (le noyau cherche à rentrer dans la culasse lorsque l’enroulement est alimenté). En première approximation, en négligeant toutes les fuites, l’inductance est inversement proportionnelle à la position \(x\):
où \(S_n\) est la section du noyau. Au dénominateur, on remplacera \(x\) par \(x+\varepsilon\) pour modéliser les fuites et éviter la singularité en \(x=0\).
Cependant, on obtiendra un résultat plus réaliste en modélisant le parcours
du flux magnétique par un circuit magnétique à réluctances.
Pour celà, on utilisera le package Modelica.Magnetic.FluxTubes
et on pourra se baser sur l’exemple SolenoidActuator,
en particulier le composant SimpleSolenoid qui correspond exactement à ce système
(Fig. 4.6).
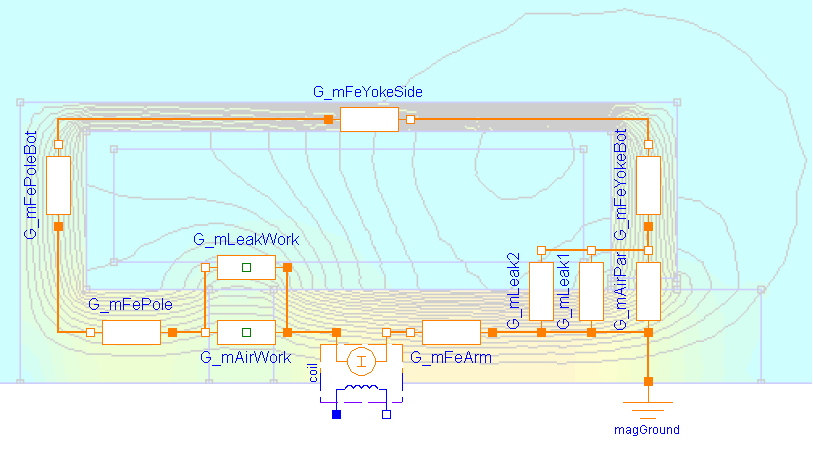
Fig. 4.6 Composants du modèle SimpleSolenoid, superposés sur la géométrie réelle du système, avec les lignes de champ magnétique calculées par la méthode des éléments finis (FEA en anglais). NB : par rapport à Fig. 4.5, seule la moitié haute est tracée, car l’objet est axisymétrique.
4.3.2. Mécanisme bielle-manivelle
Le lien entre l’électroaimant, qui est un actionneur linéaire, et l’axe de rotation qui porte les contacteurs se fait par un mécanisme bielle-manivelle.
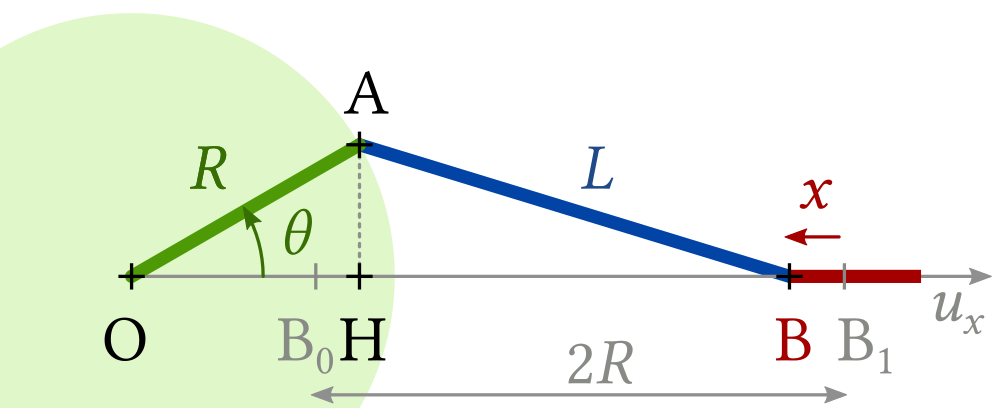
Fig. 4.7 Schéma du mécanisme bielle-manivelle
Sur le schéma Fig. 4.7, le point \(O\) est le centre de rotation de la manivelle et le point \(B\) est l’extrémité de la bielle qui effectue un mouvement de translation (c’est en \(B\) que l’actionneur linéaire se connecte). La bielle est connectée à la manivelle au point \(A\) (par une liaison pivot). On note \(R\) le rayon de la manivelle (\(OA\)) et \(L\) la longueur de la bielle (\(AB\)). La bielle est nécessairement plus longue que le rayon de la manivelle (\(L > R\) et en pratique \(L > 1.5 R\)). La position angulaire de la manivelle est notée \(\theta\).
Le mécanisme bielle-manivelle possède deux positions extrêmes :
Point mort bas : pour \(\theta = \pm\pi\), le point \(B\) est en \(B_0\) tel que \(\overline{OB_0}=L-R\)
Point mort haut : pour \(\theta = 0\), le point \(B\) est en \(B_1\) tel que \(\overline{OB_1}=L+R\)
Ainsi la course maximale du point \(B\) est égale à \(2R\) (en exploitant toute l’amplitude angulaire de la manivelle). La course maximale dépend donc du rayon de la manivelle et non de la longueur de la bielle.
Dans le cas de l’ATS, le mécanisme alterne entre deux positions symétriques autour du point mort haut, correspondant chacune à la connection à une des deux sources d’alimentations. C’est donc différent des moteurs à pistons où la manivelle effectue des rotations complètes successives. Ainsi, pour décrire le mouvement de translation du point \(B\) sur l’axe \(\vec{u}_x\), il semble pratique de définir l’origine de l’axe au point \(B_1\). On définit donc \(x = \overline{B_1B}\) la position du point \(B\) par rapport à \(B_1\) qui est négative. En particulier :
\(x=-2R\) au point mort bas (pour \(\theta = \pm\pi\))
\(x=0\) au point mort haut (pour \(\theta =0\))
Relation cinématique et efforts
Le calcul de cette position se fait en passant par le centre de rotation : \(x = \overline{B_1O} + \overline{OB} = \overline{OB} - (L+R)\).
La mesure \(\overline{OB}\) est à son tour décomposée au point \(H\) (projeté orthogonal de \(A\) sur l’axe) : \(\overline{OB} = \overline{OH} + \overline{HB}\). On calcule alors :
\(\overline{OH} = R \cos{\theta}\), et
\(\overline{HB} = \sqrt{L^{2} - R^{2} \sin^{2}{\theta}}\) (Pythagore)
Ainsi la position \(x\) vaut :
Il y a une simplification dans le cas d’une bielle longue (\(L \ll R\)). L’effet de la longueur de la bielle disparait et la translation est sinusoidale par rapport à l’angle :
Pour le calcul du couple, on s’appuie sur la conservation de la puissance: \(C\frac{d\theta}{dt} = F.\frac{dx}{dt}\).
On obtient donc
où \(\rho\), qui est la variation de la position avec l’angle \(\frac{dx}{d\theta}\), vaut :
Il y a, de même que pour la position, une simplification dans le cas d’une bielle longue :
Sur le tracé du couple Fig. 4.8, on observe en particulier l’annulation du couple aux points morts hauts et bas (quelle que soit la longueur de la bielle).
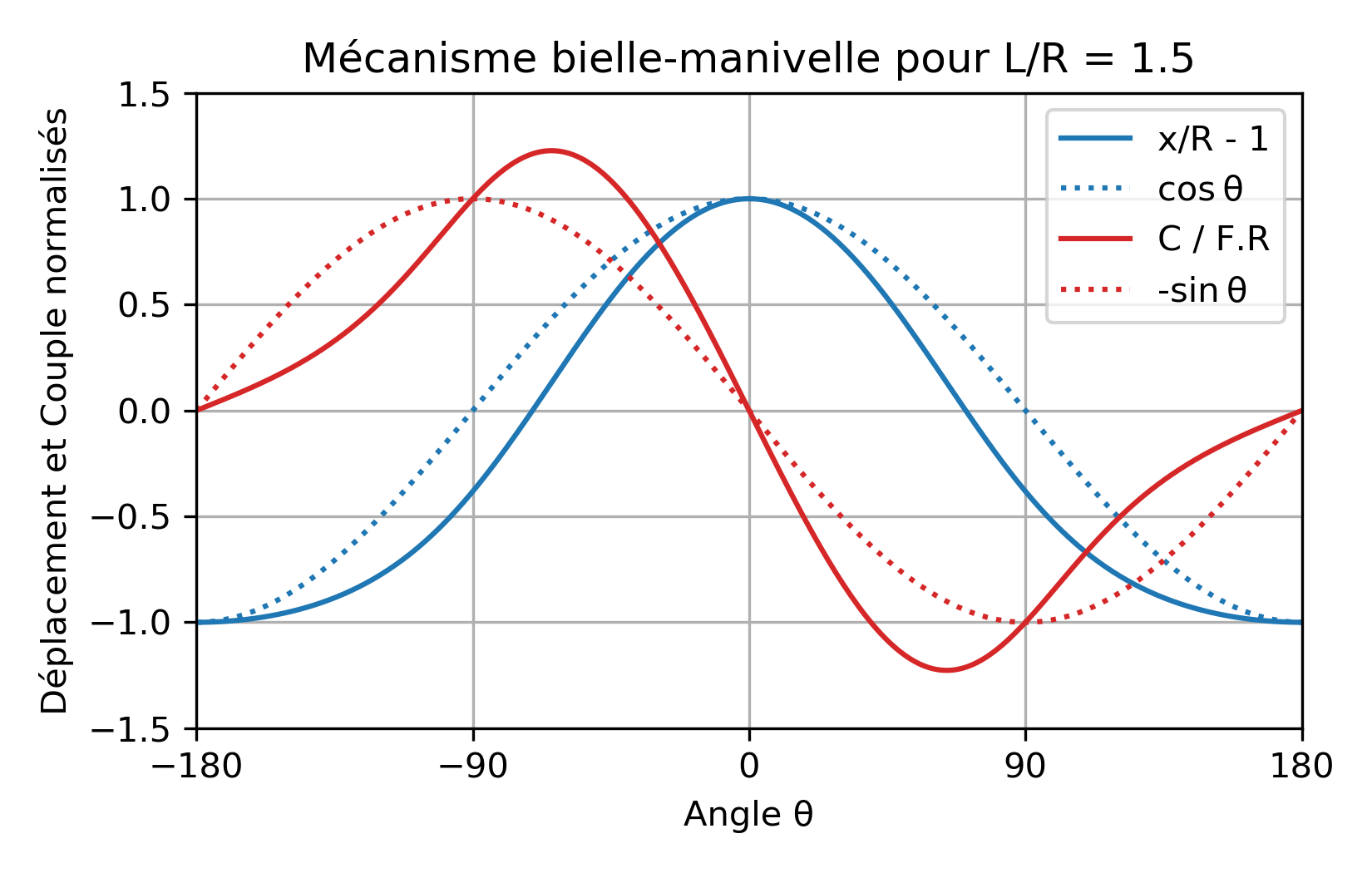
Fig. 4.8 Tracé du déplacement (bleu) et du couple (rouge) d’un mécanisme bielle-manivelle. Trait plein : bielle très courte (\(L/R = 3/2\)). Trait pointillé : bielle longue (\(L \ll R\)). Le déplacement a été recentré (translation de +1 rayon) et normalisé par le rayon. Le couple a été normalisé par le rayon et la force de translation.
Réference :
Page Wikipédia Système bielle-manivelle, mais avec des notations/définitions différentes en particulier pour l’angle.