3. Drone quadrirotor

Il s’agit de modéliser un drone quadrirotor/quadcopter, c-à-d le petit engin volants le plus populaire depuis quelques années.

Le modèle devra faire apparaître la mécanique en rotation des hélices ainsi que la mécanique en translation du corps (ou bien la mécanique 3D de l’ensemble), avec l’action de l’air sur les hélices. L’aspect électrique des moteurs n’est pas demandé (pas interdit non plus). Par ailleurs, un asservissement permettra au drone de se maintenir sa position.

3.1. Ressources techniques

3.1.1. Hélice

Objectif: modélisation la traction du drone avec une hélice. En particulier, il s’agit de calculer:

$T$ : la force de poussée (thrust) que l’hélice exerce sur le quadcopter
$P$ : la puissance absorbée par l’hélice pour exercer cette poussée.
- Elle correspond à la puissance mécanique consommée par l’hélice sur l’arbre moteur. Pour une vitesse de rotation données, la connaissance de cette puissance équivaut à la connaissance du couple résistant exercé par l’hélice ( $P = C . Ω$ )
- Elle est supérieure à la puissance utile fournit par l’hélice ( $P_{u} = T . v$ ). Le ratio $P_{u} / P$ est le rendement de l’hélice.

Pour calculer ces deux grandeurs, on peut s’appuyer sur les données constructeurs et sur des lois de similitudes. La caractérisation des hélices et typiquement donnée par deux coefficients adimensionnels.

Coefficient de poussée, qui est la poussée sous forme adimensionnelle :

C_{t} = \frac{T}{ρ N^{2} D^{4}}

Coefficient de puissance, qui est la puissance absorbée sous forme adimensionnelle :

C_{t} = \frac{P}{ρ N^{3} D^{5}}

Ces définitions font intervenir la masse volumique de l’air $ρ$ (~1.2 kg/m3), le paramètre $D$ , diamètre de l’hélice et la variable $N = Ω / 2 π$ , la vitesse de rotation en tours/seconde.

L’intérêt de ces coefficients, c’est qu’ils dépendent de la forme de l’hélice (le ratio du pas de l’hélice sur diamètre), mais peu de sa taille (diamètre). Ces coefficients ne sont cependant pas constants, ils dépendent de la vitesse de déplacement du quadcopter et de la vitesse de rotation de l’hélice, mais ils varient en fait principalement avec le ratio de ces deux vitesses. On définit ainsi l’avance (adimensionnelle) :

J = \frac{v}{N . D}

et les hélices sont alors caractérisées par la données de $C_{t} (J), C_{p} (J)$ . Par exemple Fig. 3.2, on a tracé les coefficients d’une hélice “10″×4.7″ Slow Flyer” (diamètre $D$ = 10″ = 0.254 m, et pas d’hélice de 4.7″) du fabricant APC, et ils sont a priori extrapolables à des hélices dont le pas relatif (pas/diamètre) vaut environ 0.5.

On observe typiquement que la poussée est maximale à vitesse de déplacement nulle ( $v = 0$ donc $J = 0$ , en vol stationnaire) et décroît avec $v$ et $J$ . La puissance décroit aussi, mais moins vite (ce qui fait que le rendement $P_{u} / P$ , non tracé ici, est maximal dans l’intervalle [0.4 0.6]).

Pour les besoins du projet, voici une approximation polynômiale raisonnable (tracée Fig. 3.2) des coefficients de l’hélice APC 10″×4.7″ :

C_{t} (J) \approx 0.1435 - 0.10305 J - 0.11730 J^{2}

C_{p} (J) \approx 0.0617 - 0.0238 J - 0.11922 J^{2}

Avec ces polynômes et en utilisant la définition des coefficients, on peut calculer la poussée et la puissance fonction des variables $v, N, D, ρ$ . À noter que cette hélice n’est pas sensée dépasser la vitesse de 6500 tr/min (cause : résistance mécanique à l’effort centrifuge et/ou vitesse en bout de pale $D / 2. Ω$ qui doit rester nettement subsonique).

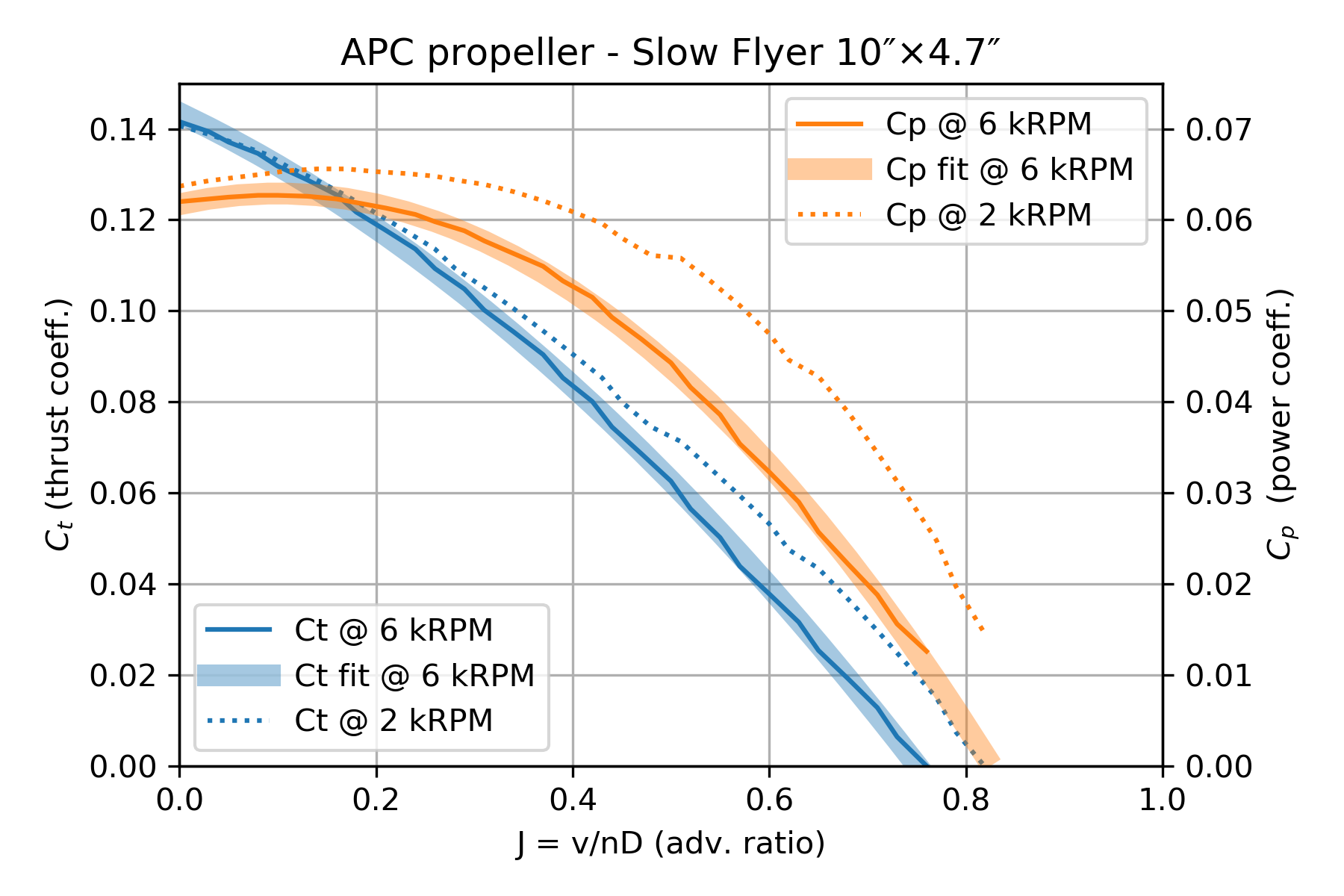
_images/Propeller_APC10x47SF.png — Fig. 3.2 Coefficients de traction $C_{t}$ et de puissance $C_{p}$ pour une hélice “10″×4.7″ Slow Flyer” du fabricant APC, d’après sa base APC Propeller Performance Data. Modélisation par des polynômes d’ordre 2 de $C_{t} (J), C_{p} (J)$ pour les données à 6000 tr/min.

Remarque : Les coefficients $C_{t}, C_{p}$ sont mesurés dans une soufflerie (ou en simulation pour les données APC) en faisant varier la vitesse $v$ pour une vitesse de rotation $N$ donnée (ou inversement). Normalement, les coefficients fonction de $J$ ne doivent plus dépendre de $N$ ou $v$ , mais on voit Fig. 3.2 qu’en réalité les coefficients obtenus à 6000 tr/min et 2000 tr/min sont un peu différents. Pour ce projet, on pourra négliger cette subtilité, surtout qu’à faible vitesse ( $J \approx 0$ , lorsque le drone est en vol stationnaire), la différence est très faible.

Références :

Blog “Aerotrash - Aéromodélisme expérimental”, articles
- Les hélices pour les nuls
Site “Aéromodélisme RC - Techniques et conception”, article La traction et les hélices